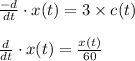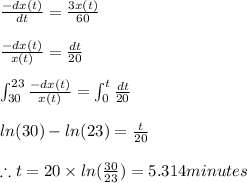Question

A tank initially contains 60 gallons of brine, with 30 pounds of salt in solution. Pure water runs into the tank at 3 gallons per minute and the well-stirred solution runs out at the same rate. How long will it be until there are 23 pounds of salt in the tank? Answer: the amount of time until 23 pounds of salt remain in the tank is minutes.

Answer 1

The time in which the amount of in which the amount of salt reduces to 23 pounds is 5.314 minutes.

Explanation:

Let the amount of salt at any time in the tank be x(t)

Let the volume of brine in the tank at any time be v(t)

The initial conditions are

`i)x(o)=30pounds\\\\ii)v(0)=60gallons`

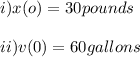
Now the concentration 'c' of brine at any time in the tank is

`c(t)=(x(t))/(v(t))`

Now since the rate of at which the water enters the tank equals the rate at which the water leaves the tank thus the volume of the brine in the tank will not change

Hence concentration of brine in the tank at time 't' is

`c(t)=(x(t))/(60)`

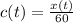
Now the rate at which the salt leaves the tank equals the rate at which the concentration of the brine decreases

Thus we have

`(-d)/(dt)\cdot x(t)=3* c(t)\\\\(d)/(dt)\cdot x(t)=(x(t))/(60)`

`(-dx(t))/(dt)=(3x(t))/(60)\\\\(-dx(t))/(x(t))=(dt)/(20)\\\\\int_(30)^(23) (-dx(t))/(x(t))=\int _(0)^(t) (dt)/(20)\\\\ln(30)-ln(23)=(t)/(20)\\\\\therefore t=20* ln((30)/(23))=5.314minutes`