Explanation:
Let's assume that
 is rational,
is rational,
So, it should be expressed in the form of
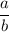
where a and b are two prime integers.
So, we can write,

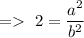
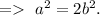
As
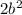 represents a even number,
represents a even number,
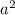 must also be even.
must also be even.
Since
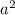 is even number, so a is also an even number.
is even number, so a is also an even number.
Let assume again that a=2c
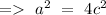

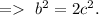
As
 is even, so
is even, so
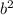 is also an even number, and so is b.
is also an even number, and so is b.
And since and b both are even number here, two even numbers can not be relatively prime, so
 can not be expressed in the form of
can not be expressed in the form of
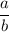 . So,
. So,
 is considered as an irrational number.
is considered as an irrational number.