Question

Solve the following system of linear equations: 3x1+6x2+6x3 = -9 -2x1–3x2-3x3 = 3 If the system has infinitely many solutions, your answer may use expressions involving the parameters r, s, and t. O The system has at least one solution x1 = 0 x2 = 0 X3 = 0 O O

Answer 1

The system has infinite solutions and the set the solutions is
`\{(x_1,x_2,x_3)=(-13,5-t,t)\in\mathbb{R}^3: t\in \mathbb{R}\}`

Explanation:

Consider the augmented matrix of the system:
`\left[\begin{array}{cccc}3&6&6&-9\\0&1&1&5\end{array}\right]`.

Now we will find the reduced echelon form of the matrix.

1. We subtract from row 2, 2/3 of row 1 and we obtain the matrix
`\left[\begin{array}{cccc}3&6&6&-9\\0&1&1&5\end{array}\right]`.

2. We multiply the row 1 of the matrix that we obtained in the previous step by 1/3 and we obtain the matrix
`\left[\begin{array}{cccc}1&2&2&-3\\0&1&1&5\end{array}\right]` that is the reduced echelon form of the system matrix.

Now we use backward substitution for find the solution:

Observe that the matrix reduced echelon form of the system matrix has a free variable, then the system has infinite solutions.

1.
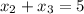`x_2+x_3=5`, then
`x_2=5-x_3`

2.
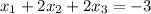`x_1+2x_2+2x_3=-3`, replacing the value of x_2,
`x_1= -2x_2-2x_3-3=-2(5-x_3)-2x_3-3=-10+2x_3-2x_3-3=-13`

Then the set of solutions is
`\{(x_1,x_2,x_3)=(-13,5-t,t)\in\mathbb{R}^3: t\in \mathbb{R}\}`