Answer:
You can prove this statement as follows:
Explanation:
An odd integer is a number of the form
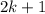 where
where
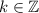 . Consider the following cases.
. Consider the following cases.
Case 1. If
 is even we have:
is even we have:
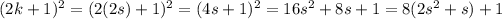 .
.
If we denote by
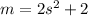 we have that
we have that
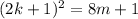 .
.
Case 2. if
 is odd we have:
is odd we have:
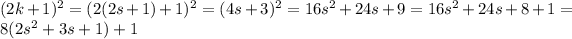 .
.
If we denote by
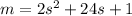 we have that
we have that
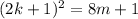
This result says that the remainder when we divide the square of any odd integer by 8 is 1.