Question

The monthly demand for a product is normally distributed with mean = 700 and standard deviation = 200.

1. What is probability demand will exceed 900 units in a month?

2. What is probability demand will be less than 392 units in a month?

Answer 1

Given :The monthly demand for a product is normally distributed with mean = 700 and standard deviation = 200.

To Find :

1. What is probability demand will exceed 900 units in a month?

2. What is probability demand will be less than 392 units in a month?

Solution:

`\mu = 700 \\\sigma = 200`

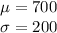
We are supposed to find probability demand will exceed 900 units in a month.

Formula :
`z=(x-\mu)/(\sigma)`

We are supposed to find P(Z>900)

Substitute x = 900

`z=(900-700)/(200)`

`z=1`

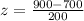
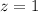
Refer the z table.

P(Z<900)=0.8413

P(Z>900)=1-P{(Z<900)=1-0.8413=0.1587

So, the probability that demand will exceed 900 units in a month is 0.1587.

Now we are supposed to find probability demand will be less than 392 units in a month

We are supposed to find P(Z<392)

Substitute x = 392

`z=(392-700)/(200)`

`z=-1.54`

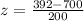
refer the z table

P(Z<900)=0.0618

So, probability that demand will be less than 392 units in a month is 0.0618.