Question

Verify that the function(s) solve the following differential equations (DES): a) y' = -5y; y = 3e-5x b) y' = cos(3x); y = į sin(3x) + 7 c) y' = 2y; y = ce2x , where c is any real number. d) y" + y' – 6y = 0 ; yı = (2x, y2 = (–3x e) y" + 16y = 0; yı = cos(4x), y2 = sin(4x)

Answer 1

Answer: So, here we need to verify that the given functions are solutions for the given differential equations, this is:

a) y' = -5y; y = 3e-5x

if
`y = 3*e^(-5x)` →
`y' = (dy)/(dx) = -5*3*e^(-5x) = -5y`

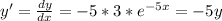
So it's true!

where i used the fact that if :
`f(x) = e^(a*x)  ------>  df/dx = a* e^(a*x)` where a is any number.

b) y' = cos(3x); y = į sin(3x) + 7

if y = į sin(3x) + 7 →
`(dy)/(dx) = 3*j*cos(3x) + 0 = j*3cos(3x)`

the equality is only true if j = 1/3.

c) y' = 2y; y = ce2x

if y =
`c*e^(2x)` →
`(dy)/(dx) = 2*c*e^(2x) = 2*(c*e^(2x)) = 2*y`

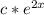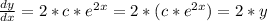
So the function is a solution for the differential equation.

d) y" + y' – 6y = 0 ; yı = (2x), y2 = (–3x )

Here we have two functions to test; is easy to se that in both cases y'' = 0, because both are linear functions, so we need to solve: y' - 6y = 0

if the functions are the 2x and -3x, then this never will be true, because when you derive y with respect of x you only will get a constant (y1' = 2 and y2' = -3), and the difference y' - 6y = 0 (2 - 12x = 0 for the first function) will only be true for some value of x, if the functions are wrong.

e) y" + 16y = 0; yı = cos(4x), y2 = sin(4x)

if y = cos(4x) →
`(dy)/(dx) = -4*sin(4x) --> (d^(2)y )/(dx^(2) )  = -16*cos(4x)`

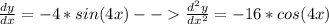
so y'' + 16y = -16cos(4x) + 16cos(4x) = 0

so y = cos(4x) is a solution

if y = sin(4x) →
`(dy)/(dx) = 4*cos(4x) --> (d^(2)y )/(dx^(2) )  = -16*sin(4x)`

then: y'' + 16y = -16sin(4x) + 16sin(4x) = 0

So again; y = sin(4x) is a solution.