Answer: a) 4, b) 13 and c) 17
Explanation:
Since we have given that
Number of elements in A = 9
Number of elements in B = 4
a) What is the largest possible value for A∩B.
Since B has only 4 elements.
So, As largest possible, it can be B⊆A.
So, Largest possible value for A∩B = 4
(b) What is the largest possible value for AUB?
If suppose A∩B = Ф
n(A∩B) = 0
So, it becomes,
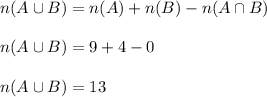
So, the largest possible value for A∪B = 13
(c) What is the value of AU B+A∩B?
|A∪B|+|A∩B|=13+4=17
Hence, a) 4, b) 13 and c) 17