Question

2. A landlord wants to acquire an additional apartment building for $250,000. The new building

contains eight apartment units, which will each rent for $500 per month. The bank is willing to
loan the landlord the money for a long-term, 30-year loan at a 5.5 percent interest rate.
Calculate the monthly payment and explain whether taking this loan for the new building is a
smart business decision. (10 points)

Answer 1

monthly payment is about $1422 (rounded)

"taking this loan would be a smart decision because even after paying off the loan, he is still making a handsome profit (because his income per month is more than his loan payment)."

Explanation:

The loan is an annuity so we use the formula for annuity to find the monthly payments he has to make.

`PV=C*(1-(1+r)^(-n))/(r)`

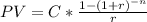
Where

PV is present value of the loan (250,000)

C is the monthly payment (what we are trying to find)

n is the number of months (30 years * 12 = 360 months)

r is the rate of interest per month ( i = 5.5%/12 = 0.0046)

Putting these values, we solve for C:

`PV=C*(1-(1+r)^(-n))/(r)\\250,000=C*(1-(1+0.0046)^(-360))/(0.0046)\\250,000=C*(1-1.0046^(-360))/(0.0046)\\250,000=C*175.7332\\C=1422`

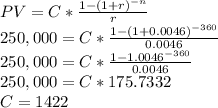
So monthly payment is about $1422 (rounded)

Since, each of the 8 apartments are going to be rented out at 500, total monthly income would be 8 * 500 = $4000

taking this loan would be a smart decision because even after paying off the loan, he is still making a handsome profit (because his income per month is more than his loan payment).