Question

Use a direct proof to show that the product of two odd integers is odd.

Answer 1

The proof itself

Explanation:

We can define the set of all even numbers as

`E = \{ a \in \mathbb{Z} \setminus a = 2.k , k\in \mathbb{N}\}`

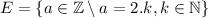
This is, we can define all even numbers as the set of all the multiples of
`2`

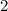
As for the odd numbers, we can always take every even number and sum one to each one. This is

`O = \{ a\in \mathbb{Z} \setminus a=2.k+1,k\in\mathbb{N}_(0)\}`

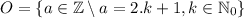
Note that
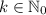`k\in\mathbb{N}_(0)`(the set of all natural numbers adding the zero) so that for
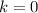`k=0` then
`a=1`

Now, given 2 odd numbers
`a` and
`b` we can write each one as follows:

`a = 2k+1\\b = 2l+1\\k,l \in\mathbb{N}_(0)`

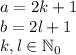
And then if we multiply them with each other we obtain:

`a.b = (2k+1).(2l+1)\\= 4kl+2k+2l+1\\= 2(2kl+k+l) + 1\\= 2k'+1 \\where\ k'=2kl+k+l`

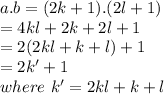
Then we have that
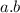`a.b` is also an odd number as we defined them.