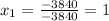Question

Let A be as above, consider Ax = b where b = (31, 2, 21, 11). Find x1 using Cramer’s rule. (You may use MATLAB/Octave to compute the determinants, but write out what you are computing.).

Matrix a= 8 6 -3 20

4 2 -5 -7

8 2 7 20

4 2 -11 -4

Answer 1

`x_1=1`

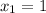
Explanation:

The matrix of the system of equations is
`A=\left[\begin{array}{cccc}8&6&-3&20\\4&2&-5&-7\\8&2&7&20\\4&2&-11&-4\end{array}\right]`.

Remember that using Cramer's Rule
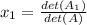`x_1=(det(A_1))/(det(A))`, where
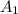`A_1` is the same matrix A change the first column of A by b. Then
`A_1=\left[\begin{array}{cccc}31&6&-3&20\\2&2&-5&-7\\21&2&7&20\\11&2&-11&-4\end{array}\right]`.

Using Octave we calculate the determinants and obtain that det(A)=-3840 and
`det(A_1)=-3840`.

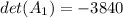Then
`x_1=(-3840)/(-3840)=1`