Answer:
(a) 210
(b) 21
(c) 86
Explanation:
(a)
We need to find how many 10-bit strings there are with only 4 bits = 1.
As the order does not matter, this number is a combination of 10 bits taken 4 at a time (those that are equal to 1)
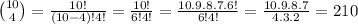
So, there are 210 10-bit strings of weight 4
(b)
As the 10-bit strings start with 101, we need a 7-bit tail with only 2 bits =1.
The order does not matter, so this a combination of 7 taken 2 at a time
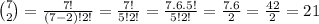
And there are 21 10-bit strings of weight 4 starting with 101
(c)
Let's compute first the number of 10-bit strings starting with 101 and having weight 5.
In this case, we need a 7-bit tail with only 3 bits =1.
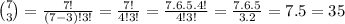
Now, the 10-bit strings ending with 11. In this case, we need a 8-bit string with only 3 bits =1.
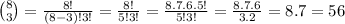
The number of 10-bit strings of weight 5 starting with 101 or ending with 11, would be 35+56 subtracting the strings starting with 101 and ending with 11, which were counted twice.
But these are 5-bit strings with only 1 bit =1, and there are 5.
So, the number of 10-bit strings of weight 5 starting with 101 or ending with 11 or both is
35+56-5 = 86.