Answer: 180
Explanation:
Given : A bag contains three red marbles, five green ones, one lavender one, two yellows, and six orange marbles.
The number of ways to choose one thing out of n is given by:-
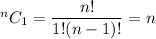
Number of ways to choose one red marble out of 3=
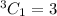
Number of ways to choose one green marble out of 5=
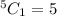
Number of ways to choose one yellow marble out of 2=
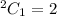
Number of ways to choose one orange marble out of 6=
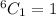
By using the Fundamental counting principle , we have
The number of sets of four marbles include one of each color other than lavender will be :-
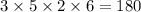
Hence, the number of sets of four marbles include one of each color other than lavender =180