Answer:
The smallest xx-intercept is

The largest xx-intercept is
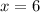
The yy-intercept is
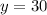 .
.
Explanation:
Given a quadratic function in the following format:
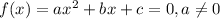
The x-values of the x-intercepts are
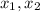 , given by the following formulas.
, given by the following formulas.
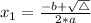
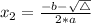
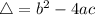
We have that:
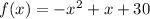
This is not in the format above. I will multiply by (-1), so we have:
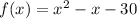
So,

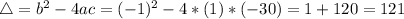
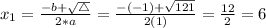

This means that
The smallest xx-intercept is

The largest xx-intercept is
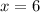
The y-intercept is the value of f(x) when x = 0. So
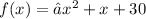
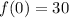
The yy-intercept is
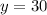 .
.