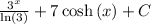Answer:
The most general anti-derivative of the function is
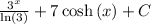
Explanation:
Definition. An anti-derivative of a function f(x) is a function whose derivative is equal to f(x). That is, if F′(x) = f(x), then F(x) is an anti-derivative of f(x).
We can use this theorem
If F is an anti-derivative of f on an interval I, then the most general anti-derivative of f on I is
F(x) + C,
where C is an arbitrary constant.
and
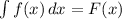 means
means
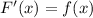
To find the anti-derivative of a function you need to follow these steps:
- Apply the sum rule
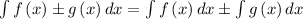
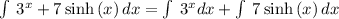
- The anti-derivative of
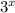 is
is
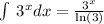
Because
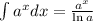
- The anti-derivative of
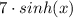 is
is
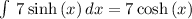
Because
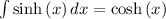
So the most general anti-derivative of the function is