Question

(a) Find the number of three-digit palindromes with a hundreds digit of 1. (b) Find the number of three-digit palindromes with a hundreds digit of 2. (c) Find the total number of three-digit palindromes. Problem 6.11: (a) Find the prime factorization of 436995. (b) The product of two positive three-digit palindromes is 436995. What is their sum? (Source: MATHCOUNTS)

Answer 1

(a) 10, (b) 10, (c) 90

6.11 (a)
`436995=3^4.5.13.83`

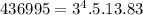
6.11 (b) 1332

Explanation:

(a)

A palindrome number is a number that reads the same forwards and backwards.

For example 232, 1331, 456654 are palindrome numbers.

A three-digit palindrome with a hundreds digit of 1 must be in the form

1n1

where n=0,1,2,3,4,5,6,7,8,9

So there are ten (10) three-digit palindromes with a hundreds digit of 1

Namely, 101, 111, 121, 131, 141, 151, 161, 171, 181 and 191

(b)

This problem is pretty much like problem (a)

There are ten (10) three-digit palindromes with a hundreds digit of 2:

202, 212, 222, 232, 242, 252, 262, 272, 282 and 292

(c)

We have 10 three-digit palindromes with a hundreds digit of 1, 10 more with a hundreds digit of 2, and so on until 9.

In total we have

9 times 10 = 90 three-digit palindromes.

(d)

436995 is a multiple of 5 because it ends in five

436995/5 = 87399

87399 is a multiple of 3 because the sum of its digits is multiple of 3

87399/3 = 29133

29133/3 = 9711

9711/3 = 3237

3237/3 = 1079

1079 is not prime because 1079 = 13 times 83

Both 13 and 83 are primes so

`436995=3^4.5.13.83`

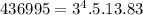
(e)

Using trial and error and the prime factorization of 436995, we find that the only three-digit palindromes whose product is

436995 are

`3^2.83=747`

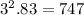
and

`3^2.5.13=585`

The sum of these 2 palindromes is 747+585 = 1332