Question

GL (n, R), the set of invertible nxn matrices with real entries, is a group under matrix multiplication. Determine if the nxn matrices with determinant -1 or 1 is a subgroup. If not, which property does not hold?

Answer 1

Let
`S=\{M\in GL(n,r): det(M)=\pm1\}`

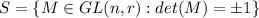
The subset S is a subgroup of GL(n,R) if satisfies:

1. The identity matrix
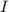`I` belong to S.

2. If A and B are in S then AB is in S.

3. If A is belong to S then
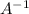`A^(-1)` belongs to S.

Let's see if S satisfies these conditions.

1. We know that
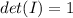`det(I)=1`, then
`I\in S`.

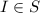2. Let A and B in S.
`det(AB)=det(A)det(B)=(\pm1)( \pm 1)=\pm 1`

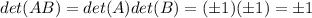
Then AB is in S.

3. Let
`A\in S`,
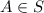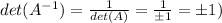`det(A^(-1))=(1)/(det(A))=(1)/(\pm 1)=\pm 1)`, then
`A^(-1)\in S`.

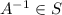Since S satisfies all conditions then S is a subgroup of GL(n,R).