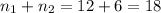Answer with Step-by-step explanation:
The number of marbles are as under
3 red , 3 green , 1 Lavender total = 7
Now to select five marbles from a total of 7 marbles such that at least 2 marbles are included are the sum of the following cases:
1) We select 2 exactly 2 red marbles from 3 reds and the remaining 3 marbles are selected from 4 of other colours
Thus
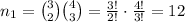
2)We select all the 3 red marbles and the remaining 2 are selected from the remaining 4 marbles

Thus the total number of ways are