Question

If a is an integer, prove that (14a + 3, 21a + 4) = 1.

Answer 1

(14a + 3, 21a + 4) = 1

Explanation:

To prove that the greatest common divisor of two numbers is 1, we use the Euclidean algorithm.

1. In this case, and applying the algorithm we would have:

(14a + 3, 21a + 4) = (14a + 3, 7a + 1) = (1, 7a + 1) = 1

2. Other way of proving this statement would be that we will need to find two integers x and y such that 1 = (14a + 3) x + (21a + 4) y

Let's make x = 3 and y = -2
`1=(14a+3)x+(21a+4)y\\1=(14a+3)(3)+(21a+4)(-2)\\1=42a+9-42a-8\\1=1`

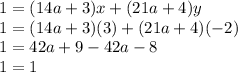
Therefore, (14a + 3, 21a + 4) = 1