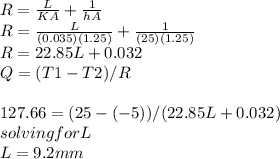Question

Clothing made of several thin layers of fabric with trapped air in between, often called ski clothing, is commonly used in cold climates because it is light, fashionable, and a very effective thermal insulator. So, it is no surprise that such clothing has largely replaced thick and heavy old-fashioned coats. Consider a jacket made up of six layers of 0.1 mm thick synthetic fabric (k = 0.026W/m.K) with 1.2 mm thick air space (k = 0.026 W/m.K) between the fabric layers. Assuming the inner surface temperature of the jacket to be 25˚C and the surface area to be 1.25 m2 , determine the heat loss through the jacket when the temperature of the outdoors is -5˚C and the heat transfer co-efficient of outer surface is 25 W/m2 .K. What would be the thickness of a wool fabric (k = 0.035W/m.K) if the person has to achieve the same level of thermal comfort wearing a thick wool coat instead of a jacket. (30 points)

Answer 1

Q=127.66W

L=9.2mm

Step-by-step explanation:

Heat transfer consists of the propagation of energy in the form of heat in different ways, these can be convection if it is through a fluid, radiation through electromagnetic waves and conduction through solid solids.

To solve any problem related to heat transfer, the general equation is used

Q = delta / R

Where

Q = heat

Delta = the temperature difference

R = is the thermal resistance by conduction, convection and radiation

to solve this problem we propose the previous equation

Q = delta / R

later we find R

`R=[tex]r=(6L1)/(AK1) +(5L2)/(AK2)+(1)/(Ah)`

`R=(6(0.0001))/((1.25)(0.026)) +(5(0.012))/((1.25)(0.026))+(1)/((25)(1.25)) =0.235 K/w`

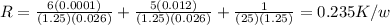
Q=(25-(-5))/0.235=127.66W

part b

we use the same ecuation with Q=127.66

Q = delta / R

Δ
`R=(L)/(KA) +(1)/(hA) \\R=(L)/((0.035)(1.25)) +(1)/((25)(1.25))\\ R=22.85L+0.032\\Q=(T1-T2)/R\\\\127.66=(25-(-5))/(22.85L+0.032)\\solving for L\\L=9.2mm`