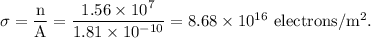Answer:
The number of excess electrons on a red blood cell =

The ratio of the mass of the extra electrons to the mass of the cell without the excess charge =
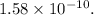
The surface charge density on the red blood cell =
 =
=
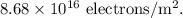
Step-by-step explanation:
Given:
- Excess charge on the red blood cell,
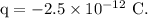
- Diameter of the red blood cell,
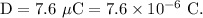
- Mass of the red blood cell,
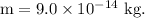
Finding the number of excess electrons on a red blood cell:
Charge on an electron,
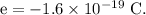
If there are n number of excess electrons on the RBC, then,

Calculating the ratio of the mass of the extra electrons to the mass of the cell without the excess charge:
Mass of 1 electron,
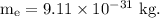
Mass of n electrons,
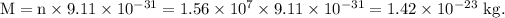
The ratio of the mass of the extra electrons to the mass of the cell without the excess charge is given as
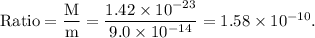
Thus, the mass of the extra electrons does not appreciably affect the mass of the cell.
Calculating the surface charge density on the red blood cell:
It is given that the red blood cells can be modeled as spheres, then, the surface area of the RBC is given as

The surface charge density of the RBC is given as:
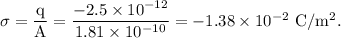
In terms of
 ,
,