Question

If (a, c) 1 and blc, prove that (a, b) = 1

Answer 1

Let
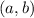`(a,b)` denote the greatest common divisor of
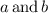`a\, \text{and}\, b`. We can prove this result as follows:

Explanation:

The Bezout's identity establishes that
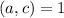`(a,c)=1` if and only if
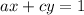`ax+cy=1` for some integers
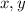`x,y`.Since
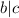`b\lvert c` then we have that
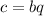`c=bq` for some
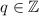`q\in \mathbb{Z}`. Then,

`ax+cy=ax+(bq)y=ax+b(yq)=ax+bz=1`

Using the result of the Bezout's identity again we can concluide that
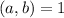`(a,b)=1`.