Answer:
(a) The speed must be greater than 20 m/s
(b) The maximun speed must be 21.6 m/s
Step-by-step explanation:
Since it's not specified, we can consider the air resistance to be zero, so this problem enters into the uniformly accelerated motion ones. For this kind of problems there's two main equations for describing the end position
 and velocity
and velocity
 as a function of time
as a function of time
 :
:

where
 and
and
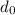 are the initial velocity and position respectivly.
are the initial velocity and position respectivly.
For this case the acceleration is the gravity
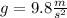 which is on the vertical axis and the initial velocity is zero since the ball is propelled on the horizontal axis. There's no aceleration on the horizontal axis.
which is on the vertical axis and the initial velocity is zero since the ball is propelled on the horizontal axis. There's no aceleration on the horizontal axis.
We must first get the time it takes the ball to drop the distance to reach the net. That is
 . Using the above equation:
. Using the above equation:
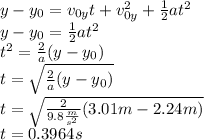
Since on the horizontal axis the motion is uniform and rectiline, the volocity
 is given by:
is given by:
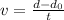
The minimun initial velocity is obtained when this final veocity is zero (the ball stops moving on the horizontal axis) and the distance is 7.93 m (the initial distance from the net), so we get

At this velocity the ball would stop at the net, so it must be greater.
For the second question, we use the same procedure as before.
In this case, the distance travelled on the vertical axis is 3.01 m, so the time it takes the ball to reach the floor is:
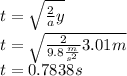
And now we use this time to get the initial velocity that would be necessary for the ball reach the end line of the court (7.93m+9m=16.93m):
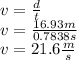
So the maximun initial velocity would be 21.6m/s since a greater one would send the ball off the court.