Question

The Call First cell phone company charges 535 per month and an additional 50.16 for each text message sent during the month. Another cell phone company, Cellular Plus, charges $45 per month and an additional $0.08 for each text message sent during the month a. How many text messages would have to be sent in a month to make both plans cost the same?

Answer 1

(The problem doesn't have solution as stated, i think you press 5 instead of $ on 535 and 50.16. With this as initial prices, they would never cost the same.)

• 125 messages.

Explanation:

We can express the charge c of the Call First company as:

`c_(cf)(m) = \$ 35 + 0.16 (\$)/(message) \ m`

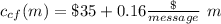
where m is the number of messages sent.

For Cellular plus

`c_(cp)(m) = \$ 45 + 0.08 (\$)/(message) \ m`.

Now, for a number of messages m' the cost will be the same

`c_(cf)(m') = c_(cp)(m)`

`\$ 35 + 0.16 (\$)/(message) \ m' = \$ 45 + 0.08 (\$)/(message) \ m'`

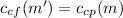
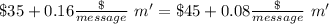
Now, we can work the equation a little

`0.16 (\$)/(message) \ m' -  0.08 (\$)/(message) \ m'= \$ 45 - \$ 35`

`(0.16 (\$)/(message) \  -  0.08 (\$)/(message)) \ m'= \$ 10`

`0.08 (\$)/(message) \ m'= \$ 10`

`m'= ( \$ 10 )/(  0.08 (\$)/(message) )`

`m'= 125 \ messages`

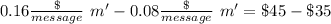
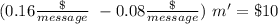
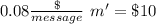
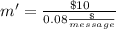
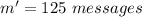
So the number of messages that needs to be sent have make both plans cost the same is 125.