Question

Two objects on the ground explode at the same time, as measured by a person at rest with respect to the ground. To the person on the ground, the explosions are separated by 5.00 m. a. Consider a person rushing past the observer on the ground, at a relative speed of 0.85 times the speed of light. Will this person agree that the explosions are simultaneous? If not, what is the time interval between them? b. Calculate the squared spacetime interval (Δs)2 = (cΔt)2-(Δx)2 for this situation. Show that it is the same for both observers, as one would expect since the spacetime interval is "Lorentz invariant." (Note that (Δs)2 can be either positive or negative, and that sometimes it is defined with the opposite signs from the ones given here.)

Answer 1

a:
`\rm -2.689* 10^(-8)\ s.`

b:
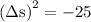`\rm \left ( \Delta s \right )^2=-25`, for both the frames.

Step-by-step explanation:

In the reference frame of a person which is at rest with respect to the ground,

The space interval of the event of explosion of two objects,
`\rm \Delta x = 5.0\ m.`

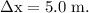
The objects explode simlultaneously in this frame, therefore, the time interval of the event,
`\rm \Delta t = 0\ s.`

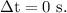
The other person is moving with the speed of 0.85 times the speed of light with respect to the ground.

`\rm v = 0.85\ c.`

Let the space and time intervals of the same event in the moving person's frame be
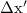`\rm \Delta x'` and
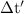`\rm \Delta t'` respectively.

Then, according to the Lorentz transformation of the space-time coordinates, the coordinates of the same event in the moving person's frame is given by

`\rm \Delta t'=\gamma \left (\Delta t-(v\Delta x )/(c^2) \right ).\\\Delta x'=\gamma (\Delta x-v\Delta t).\\\\where,\\\\\gamma = \frac{1}{\sqrt{1-(v^2)/(c^2)}}.\\\\\text{ c is the speed of light in vacuum, having value = }3* 10^8\ m/s.`

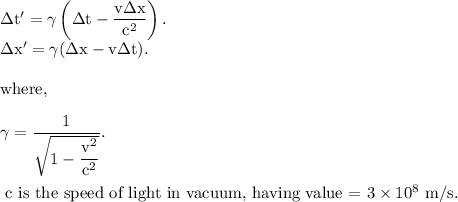
(a):

According to the Lorentz tramsfomation, the time interval of the event of explosion of the two objects in this moving person's frame is given by

`\rm \Delta t'=\frac{1}{\sqrt{1-(v^2)/(c^2)}}\left( \Delta t-(v\Delta x)/(c^2)\right )\\=\frac{1}{\sqrt{1-((0.85\ c)^2)/(c^2)}}\left( 0-(0.85\ c* 5.0)/(c^2)\right )\\=1.898* \left (-(0.85* 5.0)/(3* 10^8) \right )\\=-2.689* 10^(-8)\ s.`

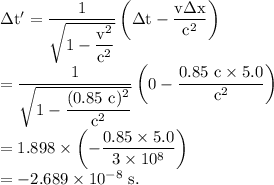
The negative time interval indicates that the second object exploded first in this frame.

The two explposions are not simultaneous in this frame.

(b):

For the reference frame of the person which is at rest with respect to the ground:

`\rm \left (c\Delta t \right )^2=\left (c\cdot 0\right )^2=0\\\left (\Delta x \right )^2=5.0^2=25.\\\Rightarrow \left (\Delta s \right )^2=0-25=-25.`

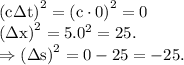
For the reference frame of the person which is moving with speed v with respect to the ground:

`\rm \Delta x'=\frac{1}{\sqrt{1-(v^2)/(c^2)}}\left( \Delta x-v\Delta t\right ) \\=1.898* (5-0)\\=9.49\ m.`

`\rm \left (c\Delta t' \right )^2=\left (3* 10^8* 2.689* 10^(-8)\right )^2=65.06\\\left (\Delta x' \right )^2=9.49^2=90.06.\\\Rightarrow \left (\Delta s' \right )^2=65.06-90.06=-25.`

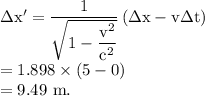
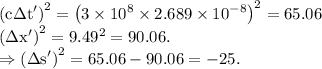
Thus, it is clear that the value of
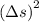`\left (\Delta s \right )^2` for both the frames are equal.