Answer:
105th term of given series is
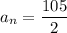
Explanation:
Given series is
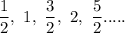
As we can see,
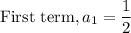
Also,
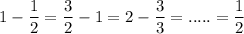
hence, we can say given series is in arithmetic progression,
with common difference,
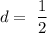
As given in question the nth term in A.P is given by
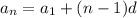
since we have to find the 105th term, so we can write
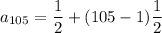
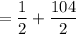
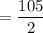
Hence, the 105th term of given series of A.P is
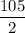 .
.