Answer:
A. The woman is relatively taller because the z score for her height is greater than the z score for the man's height.
Explanation:
Whoever has the highest z-score, is taller relative to the population of the same gender.
The z-score of a value X in a set with mean
 and standard deviation
and standard deviation
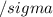 is given by:
is given by:

Solution:
Heights of men have a mean of 170 cm and a standard deviation of 6 cm. One of the tallest living men has a height of 236 cm. So the z-score of his height is:
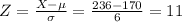
Heights of women have a mean of 161 cm and a standard deviation of 5 cm.
One of the tallest living women is 224 cm tall. The z-score of the women's height is
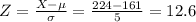
The women has a higher z-score, so she is relatively taller.
The correct answer is A