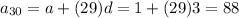Question

In an arithmetic​ sequence, the nth term an is given by the formula An=a1+(n−1)d​, where a1

is the first term and d is the common difference.​ Similarly, in a geometric​ sequence, the nth term is given by an=a1•rn−1.

Here r is the common ratio. Use these formulas to determine the indicated term in the given sequence.

The 30th term of 1​, 4​, 7​, 10​,...

Answer 1

`a_(30) = 88`

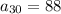
Explanation:

In this question we are given a sequence:

1, 4, 7, 10,...

If we closely examine this series it is an arithmetic progression.

An arithmetic progression is of the form
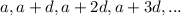`a, a+d, a+2d, a+3d, ...`, where a is the first term of the series and d is the common difference.

The
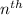`n^(th)` term of the series is given by the formula:

`a_n = a + (n-1)d`

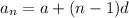
The
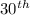`30^(th)` term of the given series is:

`a_(30) = a + (29)d = 1 + (29)3 = 88`