1 Answer

Caf · Answer 1 · 2020-07-12T12:05:21+0000

Answer:

No, irrational numbers are not closed under addition.

Explanation:

The closure property of irrational numbers under addition states that the sum of two irrational number will always be an irrational number.

That is if a and b are two irrational numbers then, their sum a + b should always be irrational.

Irrational numbers are not closed under addition.

This can be explained with the help of an example:

We know that
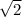$\sqrt2$ and
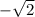$-\sqrt2$ are two irrational number.

If we consider their sum, then,

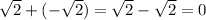
$\sqrt2 + (-\sqrt2) = \sqrt2 - \sqrt2 = 0$

But 0 is a rational number.

Hence, irrational number are not closed under addition.

Please log in or register to add a comment.