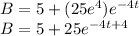Question

Find the solution to the differential equation

dB/dt+4B=20

with B(1)=30

Answer 1

The solution of the differential equation is
`B=5+25e^(-4t+4)`

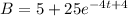
Explanation:

The differential equation
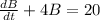`(dB)/(dt)+4B=20` is a first order separable ordinary differential equation (ODE). We know this because a separable first-order ODE has the form:

`y'(t)=g(t)\cdot h(y)`

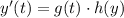
where g(t) and h(y) are given functions.

We can rewrite our differential equation in the form of a first-order separable ODE in this way:

`(dB)/(dt)+4B=20\\(dB)/(dt)=20-4B\\(dB)/(dt)=4(5-B)\\(1)/(5-B)(dB)/(dt)=4`

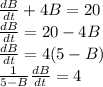
Integrating both sides

`(1)/(5-B)(dB)/(dt)=4\\(1)/(5-B)\cdot dB=4\cdot dt\\\\\int\limits {(1)/(5-B)} \, dB=\int\limits {4} \, dt`

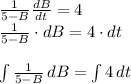
The integral of left-side is:

`\int\limits {(1)/(5-B)} \, dB\\\mathrm{Apply\:u-substitution:}\:u=5-B\\\int\limits {(1)/(5-B)} \, dB=\int\limits {(1)/(u)} \, dB\\\mathrm{du=-dB}\\-\int\limits {(1)/(u)} \,du\\\mathrm{Use\:the\:common\:integral}:\quad \int (1)/(u)du=\ln \left(\left|u\right|\right)\\-\int\limits {(1)/(u)} \,du =-\ln \left|u\right|\\\mathrm{Substitute\:back}\:u=5-B\\-\ln \left|5-B\right|\\\mathrm{Add\:a\:constant\:to\:the\:solution}\\-\ln \left|5-B\right|+C`

The integral of right-side is:

`\int\limits {4} \, dt = 4t + C`

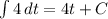
We can join the constants, and this is the implicit general solution

`-\ln \left|5-B\right|+C=4t + C\\-\ln \left|5-B\right|=4t + D`

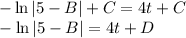
If we want to find the explicit general solution of the differential equation

We isolate B

`-\ln \left|5-B\right|=4t + D\\\ln \left|5-B\right|=-4t+D\\\left|5-B\right|=e^(-4t+D)`

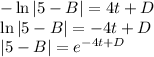
Recall the definition of |x|

`|x|=\left \{ {{x, \:if \>x\geq \>0 } \atop {-x, \:if \>x<\>0}} \right.`

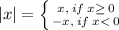
So

`\left|5-B\right|=e^(-4t+D)\\5-B= \pm \:e^(-4t+D)\\B=5 \pm \:e^(-4t+D)\\B=5\pm \:e^(-4t)\cdot e^(D)\\B=5+Ae^(-4t)`

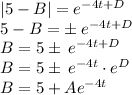
where
`A=\pm e^(D)`

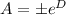
Now B(1) =30 implies

`B=5+Ae^(-4t)\\30=5+Ae^(-4)\\30-5=Ae^(-4)\\25e^(4)=A`

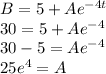
And the solution is

`B=5+(25e^(4))e^(-4t)\\B=5+25e^(-4t+4)`