Question

Find a vector i normal to the plane 2x + y + 2z = 4

Answer 1

Answer: i =2i+1j+2k

Explanation:

The parametric equation of a plane is Ax+By+Cz=D and by definition the normal vector of the plane is n=Ai+Bj+Ck, where i,j,k are the canonic vectors

Then, in this case a normal vector to the given plane is i=2i+1j+2k

To prove that a vector defined as n=Ai+Bj+Ck is normal to the plane, let V1 and V2 be two vectors that are in the plane

If V1 ∈ Ax+By+Cz=D then Aa1+Bb1+Cc1=D

If V2 ∈ Ax+By+Cz=D then Aa2+Bb2+Cc2=D

The vector V1V2=V2-V1=(a2-a1)i+(b2-b1)j+(c2-c1)k

Two vectors are normal or perpendicular if the dot product is zero.

`V2V1_(o)n=0`

`(a2-a1)i+(b2-b1)j+(c2-c1)k_(o)Ai+Bj+Cj=0\\(a2-a1)A+(b2-b1)B+(c2-c1)C=0\\Aa2+Bb2+Cc2-(Aa1+Bb1+Cc1)=0\\D-D=0`

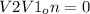
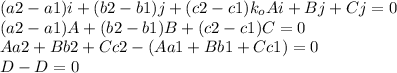
So, n is a normal vector to the plane.