Answer:
a) False
b) True
c) True
d) True
e) True
Explanation:
a) Consider the sets
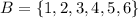 and
and
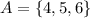 . Observe that A is a subset of B and
. Observe that A is a subset of B and
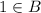 but
but
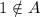
b) Any number different of 0 can be positive and negative simultaneusly. Then doesn't exist
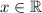 such that
such that
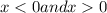 . Then the set
. Then the set
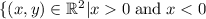 is empty.
is empty.
c) If the multiplication AB is defined and A and B are square matrices with A of size nxn, then B is the size nxn and the matrix AB is the size nxn.
d) Let A and B subsets of a set S. Since each element of A and B are in S then each element of
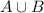 is in S. Also, if
is in S. Also, if
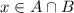 , the
, the
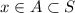 and
and
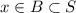 then
then
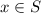 . This shows that
. This shows that
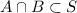 .
.
e) By definition AA=A^2