Question

A rugby player runs with the ball directly toward his opponent's goal, along the positive direction of an x axis. He can legally pass the ball to a teammate as long as the ball's velocity relative to the field does not have a positive x component. Suppose the player runs at speed 3.5 m/s relative to the field while he passes the ball with velocity v with arrowBP relative to himself. If v with arrowBP has magnitude 5.6 m/s, what is the smallest angle it can have for the pass to be legal?

Answer 1

minimum angle is 128.69°

Step-by-step explanation:

given data

player velocity with respect ground v1 = 3.5 m/s

ball velocity with respect himself v2 = 5.6 m/s

to find out

smallest angle

solution

we know ball velocity with respect field will be

ball velocity = v1 +v2

ball velocity = 3.5 + 5.6 = 9.1m/s

we consider angle that player hit ball is θ

then by as per figure triangle

cosθ =
`(v1)/(v2)`

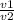
cosθ =
`(3.5)/(5.6)`

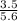
θ = 51.31

so minimum angle is 180 - 51.31 = 128.69°