Question

From a group of 7 women and 5 men, a committee consisting of 4 women and 3 menis to be formed. How many different committees are possible if

a) there are no restrictions?
b) 2 of the women refuse to serve together?

Answer 1

(a) Number of committees formed if there are no restrictions = 350

(b) Number of committees formed if 2 of the women refuse to serve together = 310

Explanation:

As per the question,

Number of women = 7

Number of men = 5

The different committees are possible if

(a) There are no restrictions

Number of committees formed

=
`^(7)C_(4) * ^(5)C_(3)`

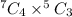
= 350

(b) 2 of the women refuse to serve together

From the 350, we must subtract the number of ways those two women serve together.

If the men and women both serve together, then 1 woman serve with 4 men.

The men are chosen

`=^(5)C_(3) = 10\ ways`,

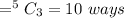So

The number we must subtract from the 350 is 4 × 10 = 40

∴ Number of committees formed = 350 - 40 = 310.