Question

Show that 2^2n-1 +1 is divisible by 3 for all n > 1.

Answer 1

Explanation:

Let's assume that

`P(n)\ =\ 2^(2n-1)+1` is divisible by 3.

for n= 1

`P(1)\ =\ 2^(2.(1)-1)+1`

= 3

Hence, P(1) is true for n=1

for n=2

`P(2)\ =\ 2^(2.(2)-1)+1`

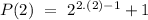
= 9, which is divisible by 3.

As we can see, P(n) is also true for n= 2.

Let's say P(n) is true for n = k

So,

`P(k)\ =\ 2^(2k-1)+1` is divisible by 3.

`=>\ P(k+1)\ =\ 2^(2(k+1)-1)+1`

`=\ 2^(2k+1)+1`

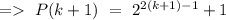
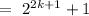
For P(n) should be true, the difference of P(k+1) and P(k) must will have divisible by 3.

So,

`P(k+1)-P(k)\ =\ 2^(2k+1)+1-(2^(2k-1)+1)`

`=\ 2^(2k-1)(2^2-1)`

`=\ 3* 2^(2k-1)`

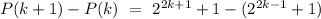
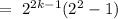
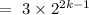
as P(k+1)-P(k) is divisible by 3.

As a result, P(n) is true for all n>1.