That depends on what
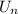 is supposed to be. Most likely it refers to some sequence.
is supposed to be. Most likely it refers to some sequence.
If
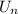 is arithmetic, then each term in the sequence differs by a constant
is arithmetic, then each term in the sequence differs by a constant
 so that
so that

Then
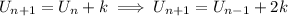
and we find
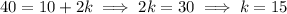
and so
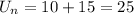
On the other hand, if
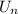 is geometric, then consecutive terms are scaled by some constant
is geometric, then consecutive terms are scaled by some constant
 so that
so that
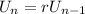
Then
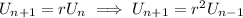
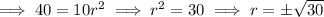
so there are two possible values for
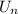 ,
,
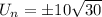
If
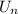 is some other type of sequence entirely, then this question would be impossible to answer without more information...
is some other type of sequence entirely, then this question would be impossible to answer without more information...