Answer:
You can proceed as follows:
Explanation:
Suppose that the matrix
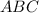 is invertible, and suppose that at least one of the matrices
is invertible, and suppose that at least one of the matrices
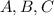 is not invertible. Without loss of generality suppose that the matrix
is not invertible. Without loss of generality suppose that the matrix
 is not invertible. Remember the important result that a matrix is invertible if and only if its determinant is nonzero. Then,
is not invertible. Remember the important result that a matrix is invertible if and only if its determinant is nonzero. Then,
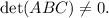
On the other hand, the determinant of a products of matrices is the product of the determinants of the matrices, that is to say,
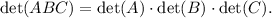
But we supposed that
 is not invertible. Then
is not invertible. Then
 . Then
. Then
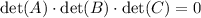 . This contradicts the fact that
. This contradicts the fact that
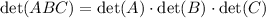
and then the three matrices
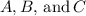 must be invertible matrices.
must be invertible matrices.