Question

Tina works for a medical technology company in sales. She travels to doctors' offices and offers them a suite of software related to patient billing and office management. She knows that 25% of the offices she visits will eventually purchase her product. She is visiting 20 offices this week. Assume the binomial is an appropriate model for the number of offices that make a purchase. On average, about how far are the possible number of sales Tina could observe from the overall mean number of sales? [Note: the question is asking about number of sales, not squared number of sales.] Select one: a. 15 b. 1.94 c. 3.37 d. 5

Answer 1

Answer: b. 1.94

Explanation:

For binomial distribution model , the formula to find standard deviation is given by :-

`\sigma=√(np(1-p))`

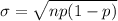
Given : The portability that the offices she visits will eventually purchase her product: p=0.25

The number of offices she visited = 20

We assume that the binomial is an appropriate model for the number of offices that make a purchase.

Then, to find the distance of the possible number of sales Tina could observe from the overall mean number of sales we find standard deviation.

`\sigma=√(np(1-p))\\\\=√(20(0.25)(0.75))\\\\=√(3.75)=1.9364916731\approx1.94`

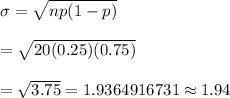
Hence, the correct answer is option (b).