Question

The heights of adult women are approximately normally distributed about a mean of 65 inches, with a standard deviation of 2 inches. If Rachael is at the 99th percentile in height for adult women, then her height, in inches, is closest to:a) 60 b) 62 c) 69 d) 70e) 74

Answer 1

Her height, in inches, is closest to 70.

Explanation:

This can be solved by the the z-score formula:

On a normaly distributed set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a value X is given by:

`Z = (X - \mu)/(\sigma)`

Each z-score value has an equivalent p-value, that represents the percentile that the value X is:

In this problem, we have that:

`\mu = 65, \sigma = 2`

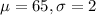
A z-score of 2.33 has a p-value of 0.9901. This means that a height with a z-score of 2.33 is in the 99th percentile.

So, what is the value of X when
`Z = 2.33`

`Z = (X - \mu)/(\sigma)`

`2.33 = (X - 65)/(2)`

`X - 65 = 4.66`

`X = 69.66`

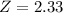
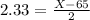
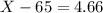
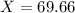
Her height, in inches, is closest to 70.