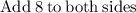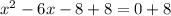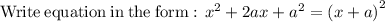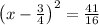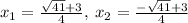Question

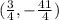
Consider the parabola given by the equation: f(x) = 4x² - 6x - 8 Find the following for this parabola: A) The vertex: Preview B) The vertical intercept is the point Preview C) Find the coordinates of the two a intercepts of the parabola and write them as a list, separated by commas: Preview It is OK to round your value(s) to to two decimal places. Get help: Video Video

Answer 1

The vertex:
`((3)/(4),-(41)/(4) )`

The vertical intercept is:
`y=-8`

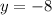
The coordinates of the two intercepts of the parabola are
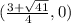`((3+√(41) )/(4) , 0)` and
`((3-√(41) )/(4) , 0)`

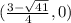
Explanation:

To find the vertex of the parabola
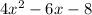`4x^2-6x-8` you need to:

1. Find the coefficients a, b, and c of the parabola equation

`a=4, b=-6, \:and \:c=-8`

2. You can apply this formula to find x-coordinate of the vertex

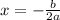`x=-(b)/(2a)`, so

`x=-(-6)/(2\cdot 4)\\x=(3)/(4)`

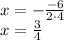
3. To find the y-coordinate of the vertex you use the parabola equation and x-coordinate of the vertex (
`f(-(b)/(2a))=a(-(b)/(2a))^2+b(-(b)/(2a))+c`)

`f(-(b)/(2a))=a(-(b)/(2a))^2+b(-(b)/(2a))+c\\f((3)/(4))=4\cdot ((3)/(4))^2-6\cdot ((3)/(4))-8\\y=(-41)/(4)`

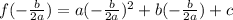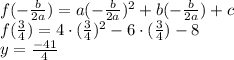
To find the vertical intercept you need to evaluate x = 0 into the parabola equation

`f(x)=4x^2-6x-8\\f(0)=4(0)^2-6\cdot 0-0\\f(0)=-8`

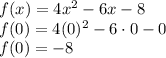
To find the coordinates of the two intercepts of the parabola you need to solve the parabola by completing the square

`\mathrm{Add\:}8\mathrm{\:to\:both\:sides}`

`x^2-6x-8+8=0+8`

`\mathrm{Simplify}`

`4x^2-6x=8`

`\mathrm{Divide\:both\:sides\:by\:}4`

`(4x^2-6x)/(4)=(8)/(4)\\x^2-(3x)/(2)=2`

`\mathrm{Write\:equation\:in\:the\:form:\:\:}x^2+2ax+a^2=\left(x+a\right)^2`

`x^2-(3x)/(2)+\left(-(3)/(4)\right)^2=2+\left(-(3)/(4)\right)^2\\x^2-(3x)/(2)+\left(-(3)/(4)\right)^2=(41)/(16)`

`\left(x-(3)/(4)\right)^2=(41)/(16)`

`\mathrm{For\:}f^2\left(x\right)=a\mathrm{\:the\:solutions\:are\:}f\left(x\right)=√(a),\:-√(a)`

`x_1=(√(41)+3)/(4),\:x_2=(-√(41)+3)/(4)`