Question

The height y (in feet) of a ball thrown by a child is y=-1/14 x^2 + 2x +3 where a is the horizontal distance in feet from the point at which the ball is thrown. (a) How high is the ball when it leaves the child's hand? Preview feet (b) What is the maximum height of the ball? Preview feet (c) How far from the child does the ball strike the ground? Preview feet Get help: Video

Answer 1

Part 1) Height of ball at launch = 3 feet.

Part 2) Maximum height achieved by ball = 17 feet

Part 3) Point at which ball strikes the ground = 29.43 feet from point of launch.

Explanation:

The height as a function of position of launch is given as

`y(x)=(-1)/(14)x^2+2x+3.............(i)`

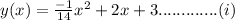
Part 1)

Since at the time the ball leaves the hand of the child the distance of the ball from point of throwing is zero thus putting x = 0 in the above equation we get

Height of throw
`y(0)=(-1)/(14)0^2+2\cdot 0+3=3`

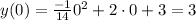
Thus the ball is at 3 feet high when it leaves the child's hand.

Part 2)

The maximum height the ball achieves can be found by maximizing the given function

Thus differentiating equation 'i' with respect to 'x' and subsequently equating to zero we get

`(dy)/(dx)=(d)/(dx)((-1)/(14)x^2+2x+3)\\\\y'(x)=(-2)/(14)x+2\\\\\therefore (-2)/(14)x+2=0\\\\x=14`

Thus the maximum value of y(x) occurs at x = 14 feet thus

`y(14)=(-1)/(14)\cdot 14^2+2* 14+3\\\\\therefore y_(max)=17feet`

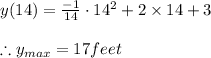
Part 3)

At the moment the ball strikes the ground it's height from the ground should be = 0

Thus equating y(x) = 0 we get

`y(x)=(-1)/(14)x^2+2x+3=0\\\\\therefore x=\frac{-2\pm \sqrt{2^(2)-4* (-1)/(14)* 3}}{2* (-1)/(14)}\\\\\therefore x_(1)=29.43\\x_(2)=-1.42`

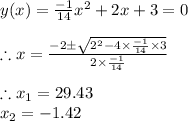
Taking the positive value we find the distance at which the ball strikes the ground equals 29.43 feet.