Consider the Quadratic function f(x) = 4x^2 - 1. Its vertex is Preview The x value of its largest x-intercept is x = The y value of the y-intercept is y = Preview Preview Previe…

Question

asked May 9, 2020 178k views

1 Answer

David Hellsing · Answer 1 · 2020-05-14T21:05:21+0000

Answer:

Its vertex is
(0,-1) .

The x value of its largest x-intercept is
(1)/(2) .

The y value of the y-intercept is
y = -1 .

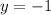Explanation:

A quadratic function in the format:

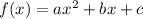
f(x) = ax^(2) + bx + c

Has the vertex
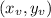(x_(v), y_(v)) given by:

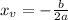
x_(v) = -(b)/(2a)

y_(v) = f(x_(v))

So

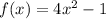f(x) = 4x^(2) - 1 , we have that:

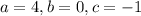
a = 4, b = 0, c = -1

So

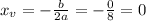
x_(v) = -(b)/(2a) = -(0)/(8) = 0

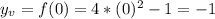
y_(v) = f(0) = 4*(0)^(2) - 1 = -1

Its vertex is
(0,-1)

The x-intercept values are the values of x when f(x) = 0;

So

f(x) = 0

4x^(2) - 1 = 0

4x^(2) = 1

x^(2) = (1)/(4)

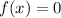
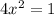
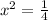
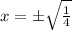
$x = \pm \sqrt{(1)/(4)}$

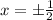
$x = \pm (1)/(2)$

The x value of its largest x-intercept is
x = (1)/(2) .

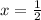The y-intercept is the value of f(x) when x = 0, so, f(0)

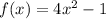
f(x) = 4x^(2) - 1

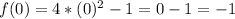
f(0) = 4*(0)^(2) - 1 = 0-1 = -1

The y value of the y-intercept is
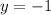y = -1 .