Question

Danny has decided to retire once he has $1,000,000 in his retirement account. At the end of each year, he will contribute $7,000 to the account, which is expected to provide an annual return of 6.2%. How many years will it take until he can retire? 40 years 36 years 43 years 39 years 38 years Suppose Danny’s friend, Hugh, has the same retirement plan, saving $7,000 at the end of each year and retiring once he hits $1,000,000. However, Hugh’s account is expected to provide an annual return of 7.9%. How much sooner can Hugh retire? 6 years 4 years 8 years 5 years 7 years After 25 years, neither Danny nor Hugh will have enough money to retire, but how much more will Hugh’s account be worth at this time? $141,056 $139,984 $109,283 $289,671 $215,877 Danny is jealous of Hugh because Hugh is scheduled to retire before him, so Danny decides to make whatever end-of-year contribution is necessary to reach the $1,000,000 goal at the same time as Hugh. If Danny continues to earn 6.2% annual interest, what annual contributions must he make in order to retire at the same time as Hugh? $7,751 $9,873 $16,452 $8,408 $13,241

Answer 1

Ans. A) Danny can retire in 38 years; B) Hugh will retire 5 years sooner (retires in 33 years; C) Hugh´s account will have $504,327.38 in 25 years, D) Danny´s annual contribution has to be $9,873.20 if he wants to retire in 33 years, like Hugh.

Step-by-step explanation:

Hi, in order to answer all this questions, we have to use the following equation.

`FutureValue=(A(1+r)^(n)-1) )/(r)`

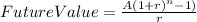
To solve the first question, we have to solve for "n" this equation, the math to this as follows.

`1,000,000=(7,000(1+0.062)^(n)-1) )/(0.062)`

`62,000=7,000(1+0.062)^(n) -7,000`

`69,000=7,000(1+0.062)^(n)`
`9.85714286=(1+0.062)^(n)`

`Ln(9.85714286)=n*Ln(1.062)`

`n=(Ln(9.85714286))/(Ln(1.062)) =38 years`

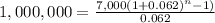
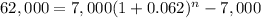
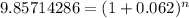
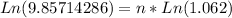
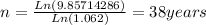
To answer B), we need to do the same process, only that we change 0.062 for 0.079, but all the process is the same.

`1,000,000=(7,000((1+0.079)^(n)-1) )/(0.079)`

`12.2857143=1.079^(n)`

`n=(Ln(12.2857143))/(Ln(1.079)) =33 years`

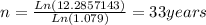
Since Danny will retire in 38 years and Hugh in 33, Hugh is going to retire 5 years sooner than Danny.

C) To find the balance in 25 years in Hughs Account, we just go ahead and use the formula to find the future value, like this.

`FutureValue=(7,000((1.079)^(25) -1))/(0.079)`

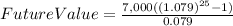
This means that FV= $504,327.38

D)in order to find the annual payment that Danny has to make in order ti retire in 33 years, just as Hugh, we need to solve the initial equation for "A".

`1,000,000=(A((1+0.062)^(33) -1))/(0.062)`

`1,000,000=A(101.284286)`
`A=(1,000,000)/(101.284286) =9,873.20`

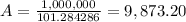
Best of luck.