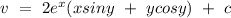Question

Prove that u(x) := e* (x COS Y – ysiny) is harmonic and find a conjugate function of u.

Answer 1

`u(x)=\ =\ e^x(xcosy\ -\ ysiny)\ \textrm{is harmonic.}`

`\textrm{conjugate function},\ v\ =\ 2e^x(xsiny\ +\ ycosy)\ +\ c`

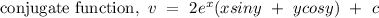
Explanation:

As given in question,

• 
  `u(x)\ =\ e^x(xcosy\ -\ ysiny)`

`=\ e^x.xcosy\ -\ e^x.ysiny`

`=>\ u'_x(x)\ =\ e^x.cosy\ +\ xe^xcosy\ -\ ye^xsiny\\\\=>\ u''_x(x)\ =\ e^xcosy+e^xcosy+xe^xcosy-e^xysiny\\\\=>\ u'_y(x)\ =\ -e^x.xsiny\ -\ e^xsiny\ -\ e^x.ycosy\\\\=>\ u''_y(x)\ =\ -xe^xcosy\ -\ 2e^xcosy\ +\ e^x.ysiny`

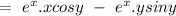
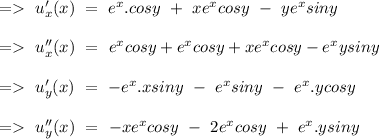
For a system to be harmonic,

`(\partial^2 u)/(\partial x^2)\ +\ (\partial^2 u)/(\partial y^2)\ =\ 0`

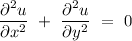
From the above calculated value we can see that

`(\partial^2 u)/(\partial x^2)\ +\ (\partial^2 u)/(\partial y^2)`

`=\ e^xcosy+e^xcosy+xe^xcosy-e^xysiny\ -\ xe^xcosy\ -\ 2e^xcosy\ +\ e^x.ysiny`

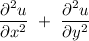
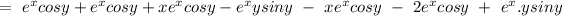
= 0

So, given function u(x) is harmonic.

Now to find conjugate function of u,

`dv\ =\ (\partial v)/(\partial x).dx\ +\ (\partial v)/(\partial y).dy`

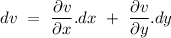
According to Cauchy-Riemen Equation,

`(\partial u)/(\partial x)\ =\ (\partial v)/(\partial y)\\\\(\partial u)/(\partial y)\ =\ -(\partial v)/(\partial x)`

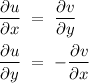
So, we4 can write the above equation as,

`dv\ =\ -(\partial u)/(\partial y)dx\ +\ (\partial u)/(\partial x)dy`

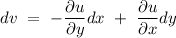
on putting the values, we have

`dv\ =\ -(-e^x.xsiny\ -\ e^xsiny\ -\ e^x.ycosy)dx\ +\ (e^x.cosy\ +\ xe^xcosy\ -\ ye^xsiny)dy`

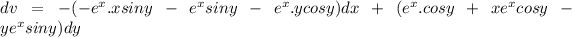
on integrating both side, we get

`\int{dv}\ =\ \int{e^x.xsiny\ +\ e^xsiny\ +\ e^x.ycosy)dx}\ +\ \int{(e^x.cosy\ +\ xe^xcosy\ -\ ye^xsiny)dy}`

`=>\ v\ =\ 2xe^xsiny\ +\ 2ye^xcosy\ +\ c`

`=\ 2e^x(xsiny\ +\ ycosy)\ +\ c`

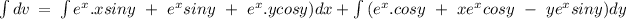
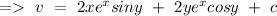
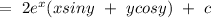
hence, the conjugate equation can be given by

`v\ =\ 2e^x(xsiny\ +\ ycosy)\ +\ c`