Question

Convert the given system of equations to matrix form

2. Use row operations to put the matrix in echelon form.

3. Find the solutions set and put in vector form.

x+y+w+z-3u=5

x-y-2w+z+2u=4 2x+0+w-z+u=3

Answer 1

The matrix form of the system of equations is
`\left[\begin{array}{ccccc}1&1&1&1&-3\\1&-1&-2&1&2\\2&0&1&-1&1\end{array}\right] \left[\begin{array}{c}x&y&w&z&u\end{array}\right] =\left[\begin{array}{c}5&4&3\end{array}\right]`

The reduced row echelon form is
`\left[\begin{array}c1&0&0&1/4&0&3\\0&1&0&9/4&-4&5\\0&0&1&-3/2&1&-3\end{array}\right]`

The vector form of the general solution for this system is
`\left[\begin{array}{c}x&y&w&z&u\end{array}\right]=u\left[\begin{array}{c}-(1)/(6)&(5)/(2)&0&(2)/(3)&1\end{array}\right]+w\left[\begin{array}{c}-(1)/(6)&-(3)/(2)&1&(2)/(3)&0\end{array}\right]+\left[\begin{array}{c}(5)/(2)&(1)/(2)&0&2&0\end{array}\right]`

Explanation:

• Convert the given system of equations to matrix form

We have the following system of linear equations:

`x+y+w+z-3u=5\\x-y-2w+z+2u=4\\2x+w-z+u=3`

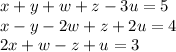
To arrange this system in matrix form (Ax = b), we need the coefficient matrix (A), the variable matrix (x), and the constant matrix (b).

so

`A= \left[\begin{array}{ccccc}1&1&1&1&-3\\1&-1&-2&1&2\\2&0&1&-1&1\end{array}\right]`

`x=\left[\begin{array}{c}x&y&w&z&u\end{array}\right]`

`b=\left[\begin{array}{c}5&4&3\end{array}\right]`

• Use row operations to put the augmented matrix in echelon form.

An augmented matrix for a system of equations is the matrix obtained by appending the columns of b to the right of those of A.

So for our system the augmented matrix is:

`\left[\begin{array}ccccc1&1&1&1&-3&5\\1&-1&-2&1&2&4\\2&0&1&-1&1&3\end{array}\right]`

To transform the augmented matrix to reduced row echelon form we need to follow this row operations:

• add -1 times the 1st row to the 2nd row

`\left[\begin{array}ccccc1&1&1&1&-3&5\\0&-2&-3&0&5&-1\\2&0&1&-1&1&3\end{array}\right]`

• add -2 times the 1st row to the 3rd row

`\left[\begin{array}c1&1&1&1&-3&5\\0&-2&-3&0&5&-1\\0&-2&-1&-3&7&-7\end{array}\right]`

• multiply the 2nd row by -1/2

`\left[\begin{array}ccccc1&1&1&1&-3&5\\0&1&3/2&0&-5/2&1/2\\0&-2&-1&-3&7&-7\end{array}\right]`

• add 2 times the 2nd row to the 3rd row

`\left[\begin{array}ccccc1&1&1&1&-3&5\\0&1&3/2&0&-5/2&1/2\\0&0&2&-3&2&-6\end{array}\right]`

• multiply the 3rd row by 1/2

`\left[\begin{array}ccccc1&1&1&1&-3&5\\0&1&3/2&0&-5/2&1/2\\0&0&1&-3/2&1&-3\end{array}\right]`

• add -3/2 times the 3rd row to the 2nd row

`\left[\begin{array}c1&1&1&1&-3&5\\0&1&0&9/4&-4&5\\0&0&1&-3/2&1&-3\end{array}\right]`

• add -1 times the 3rd row to the 1st row

`\left[\begin{array}ccccc1&1&0&5/2&-4&8\\0&1&0&9/4&-4&5\\0&0&1&-3/2&1&-3\end{array}\right]`

• add -1 times the 2nd row to the 1st row

`\left[\begin{array}ccccc1&0&0&1/4&0&3\\0&1&0&9/4&-4&5\\0&0&1&-3/2&1&-3\end{array}\right]`

• Find the solutions set and put in vector form.

Interpret the reduced row echelon form:

The reduced row echelon form of the augmented matrix is

`\left[\begin{array}ccccc1&0&0&1/4&0&3\\0&1&0&9/4&-4&5\\0&0&1&-3/2&1&-3\end{array}\right]`

which corresponds to the system:

`x+1/4\cdot z=3\\y+9/4\cdot z-4u=5\\w-3/2\cdot z+u=-3`

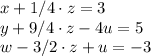
We can solve for z:

`z=(2)/(3)(u+w+3)`

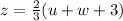
and replace this value into the other two equations

`x+1/4 \cdot ((2)/(3)(u+w+3))=3\\x=-(u)/(6) -(w)/(6)+(5)/(2)`

`y+9/4 \cdot ((2)/(3)(u+w+3))-4u=5\\y=(5u)/(2)-(3w)/(2)+(1)/(2)`

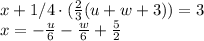
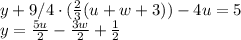
No equation of this system has a form zero = nonzero; Therefore, the system is consistent. The system has infinitely many solutions:

`x=-(u)/(6) -(w)/(6)+(5)/(2)\\y=(5u)/(2)-(3w)/(2)+(1)/(2)\\z=(2u)/(3)+(2w)/(3)+2`

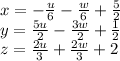
where u and w are free variables.

We put all 5 variables into a column vector, in order, x,y,w,z,u

`x=\left[\begin{array}{c}x&y&w&z&u\end{array}\right]=\left[\begin{array}{c}-(u)/(6) -(w)/(6)+(5)/(2)&(5u)/(2)-(3w)/(2)+(1)/(2)&w&(2u)/(3)+(2w)/(3)+2&u\end{array}\right]`

Next we break it up into 3 vectors, the one with all u's, the one with all w's and the one with all constants:

`\left[\begin{array}{c}-(u)/(6)&(5u)/(2)&0&(2u)/(3)&u\end{array}\right]+\left[\begin{array}{c}-(w)/(6)&-(3w)/(2)&w&(2w)/(3)&0\end{array}\right]+\left[\begin{array}{c}(5)/(2)&(1)/(2)&0&2&0\end{array}\right]`

Next we factor u out of the first vector and w out of the second:

`u\left[\begin{array}{c}-(1)/(6)&(5)/(2)&0&(2)/(3)&1\end{array}\right]+w\left[\begin{array}{c}-(1)/(6)&-(3)/(2)&1&(2)/(3)&0\end{array}\right]+\left[\begin{array}{c}(5)/(2)&(1)/(2)&0&2&0\end{array}\right]`

The vector form of the general solution is

`\left[\begin{array}{c}x&y&w&z&u\end{array}\right]=u\left[\begin{array}{c}-(1)/(6)&(5)/(2)&0&(2)/(3)&1\end{array}\right]+w\left[\begin{array}{c}-(1)/(6)&-(3)/(2)&1&(2)/(3)&0\end{array}\right]+\left[\begin{array}{c}(5)/(2)&(1)/(2)&0&2&0\end{array}\right]`