Question

Team A and Team B play each other in a best out of 7 tournament. So the team that wins 4 games first wins the tournament. How many possible sequences are there for team A to win? Examples: AAAA, AAABA, AABAA, etc.

Answer 1

There are 35 ways.

Explanation:

Consider the provided information.

In order to find the number of possible sequences we have few case:

Case I: If team A will win all 4 games without losing any match.

A A A A

There is only 1 way as you can see, Because after winning 4 games in a row no need to play again.

Case II: If team A will win 4 games out of 5 games.

A A A B A, or A A B A A, or A B A A A, or B A A A A,

Remember A A A A B this is not going to include.

That means there are 4 possible ways if team B win one match.

Case III: If team A will win 4 games out of 6 games.

It means team A needs to win 3 games from first 5 games so that after wining 6th match they win the tournament.

So the number of ways are
`(5!)/(3!2!)=10`

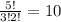
That means there are 10 possible ways if team B win two match.

Case IV: If team A will win 4 games out of 7 games.

It means team A needs to win 3 games from first 6 games so that after wining 7th match they win the tournament.

So the number of ways are
`(6!)/(3!3!)=20`

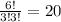
That means there are 20 possible ways if team B win three match.

Thus, the total number of ways are: 1 + 4 + 10 + 20 = 35

Hence, there are 35 ways.