Answer:
(a)
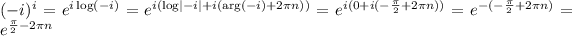 , where
, where
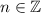
(b)
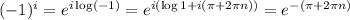 , where
, where
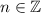 .
.
Explanation:
Let's remember the definition of complex exponents. If
 is a nonzero complex number and
is a nonzero complex number and
 is a complex number, we define
is a complex number, we define
 by
by
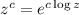
Where the
 function is the complex logarithm function. That is to say,
function is the complex logarithm function. That is to say,
 , where
, where
 . With this in mind we can calculate the given powers as follows:
. With this in mind we can calculate the given powers as follows:
(a)
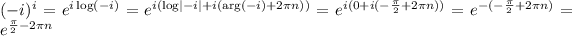 , where
, where
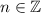
(b)
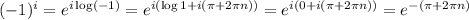 , where
, where
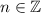 .
.
This are all the values of the given powers.