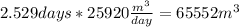Question

A lagoon is to be designed to accommodate an input flow of 0.30 m3/s of nonconservative pollutant with concentration 33.0 mg L and reaction rate constant 0.4/day. The effluent from the lagoon must have pollutant concentration of less than 12.0 mg/l. Assuming complete mixing, how long must the lagoon be?

Answer 1

The lagoon must be at least 65552 m3

Explanation:

First its we have to know the detention time that its needed for the pollutant to reduce its concentration up to 12 mg/l.

We use the formula of decay:

`C=C_(0)*exp^(-k*t)`

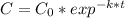
We can calculte the time as

`t = -(1)/(k)*ln((C)/(C_(0)))=  -(1)/(0.4)*ln((12)/(33))=2,529 days`

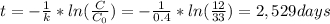
The flow of the pollutant is 0.3 m3/s, so the daily flow is

`0.3(m^(3))/(s) *86400(s)/(day) =25920 (m^(3))/(day)`

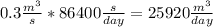
The lagoon has to be at least this volume:

`2.529 days * 25920 (m^(3))/(day) = 65552 m^(3)`