Answer:
1) The demand equation is
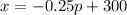
2) The price when no consumers willing to buy this commodity is $1200.
3) The quantity of the commodity would consumers take if it was free is 300 pounds.
Explanation:
Given : At a unit price of $900, the quantity demanded of a certain commodity is 75 pounds. If the unit price increases to $956, the quantity demanded decreases by 14 pounds.
To find :
1) The demand equation ?
2) At what price are no consumers willing to buy this commodity?
3) According to the above model, how many pounds of this commodity would consumers take if it was free?
Solution :
1) According to question,
p is the unit price and x is the quantity demanded for this commodity in pounds.
Let,
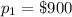 and
and
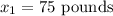
and
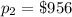 and
and

To find the demand equation we apply two point slope form,
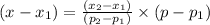
Substitute the values,
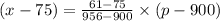
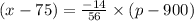
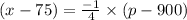
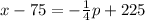
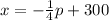
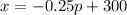
The demand equation is
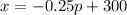
2) For no consumers,
Substitute x=0 in demand equation,
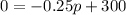
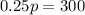
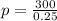
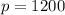
The price when no consumers willing to buy this commodity is $1200.
3) For free,
Substitute p=0 in demand equation,
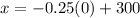
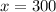
The quantity of the commodity would consumers take if it was free is 300 pounds.