Answer:
y=sin(ln(x))
Explanation:
First, we have to order the terms as follows and express y' as dy / dx:

Then, we have to integrate
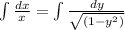
with this solution after integration:
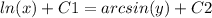
Then, we have to reorder
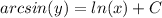
and applied Sin function on both sides
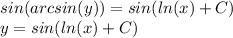
To define the value of C, we use the known point y(1)=0 and replace in the equation

The function that proves that differential equation is
