Answer:
b) 18 m/s
Step-by-step explanation:
From the exercise we got maximum height and the angle which the bait is launched.
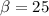 º
º
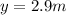
We know that at maximum height, the velocity at y-axis is 0
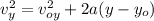
Since
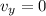
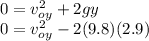

Since the bait is launched at
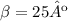
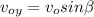
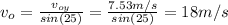
So, the answer to the problem is b